Tuesday, August 7, 2012
astro picture for the day/thought for the day/ the mathematics of the circle
credit Leonard Mercer
---------------------------------Mechanical Universe extra----------------------------------------------
==============================================================
New account of the ancient mathematics of the circle -
The mathematics of Thales was interesting because of the way the theorems related to one another, in my opinion. Similarly, for Babylonian geometric algebra and the Pythagorean theorem(which I've yet to write up!). Similarly, the mathematical story of the circle is interesting in the mathematics that is generated. Sometimes a wrong path still makes for interesting mathematics, and then the mathematics along the correct road is holy!
The earliest mathematical knowledge of the circle before the Greeks was the Babylonians. The neat thing they did was inscribe a hexagon in a circle. It's the easiest polygon construction one can do! Use the circles radius, and make equivalent lines starting from one point of the circle where a given radius meets the circle, let the other point of the equivalent line meet the circle, and the next line starts from that endpoint, all the way around the inside of the circle, and you get a six sided figure. So, the Circumference of the hexagon is 6, and the diameter is 2, so, circumference is approximated as 3.
The Babylonians hit on the insight that different size circles have the same ratio of diameter to circumference. C/D="pi", or C=(pi)D. Either way, "Pi" come out of know-where, almost Jacob Bronowski 'inferred units like'(see my nature and origin of mathematical knowledge; third post of this blog!). It also hides behind some mysterious symbolism much as the square root of two! But, that's getting ahead of the story.
In a connection between the mathematics of Thales and that of Pi, Thales most exciting theorem, "angles in a semi-circle are right angles" is used to by a Hippocrates to solve the 'quadrature of the lune'.
Hippocrates is also credited, by the Greeks, to having composed an 'Elements' like Euclid did hundreds of years later. Thales either discovered deductive proof, or as some evidence was found and communicated by Van Der Waerden, in his "Geometry and Algebra in Ancient Civilizations" book, Thales learned from a grapevine coming all the way from India! Then, Thales taught Pythagoras, and the Greek mathematical awakening was lit. The famous example of deductive reasoning is Plato's syllogism "All men are mortal . . . Socrates is a man . . . therefore, Socrates must die". The Deduction is two assumptions(in this case), and then a third conclusion that follows 'logically'! The Greeks, apparently, saw that one could perhaps try to prove everything deductively from a finite set of axioms/postualtes. The two assumptions mentions in the above Plato syllogism are like these axioms for that deduction. Hippocrates appears, as far as anyone can tell, to be the first to postulate all the results of Greek mathematics up to his lifetime; essentially, he codified all of Pythagorean mathematics! The result is lost. In fact, the only original Greek mathematics that has come down to us is a result of Hippocrates - the Quadrature of the Lune. This was about 440 B.C. This was a major result at the time of Greek mathematics. It was also before Athenian Greek history.
The Greeks at this time hoped to tame the circle by squaring it. In fact, the Greeks hoped to square everything! Because the calculation of the square is easy, if they could turn everything into a square, then, they can solve everything in the universe! The ancient mathematics of the circle is kind of hard to put in a straight line. Because there's connections between the mathematics of squaring everthing and the irrationality of the square root of two, I'm going to back up and present that mathematics, and then get back to showing Hippocrates "Quadrature of the Lune."
- One of the greatest Greek theorems before Hippocrates 'Quadrature of the Circle" is Pythagorases theorem about right triangles. The right angles triangle has a right angle in it which generates a hypotenuse diagonal side. A right angle is one that is a 90 degrees angle. The Pythagoras is credited for proving this deductively. The Babylonians may have proved a linear case of this.
Start with a square, draw two diagonals inside the square, generating four equal triangles. On one side of the square, make a triangle on top of the square equal to one of those triangles. Draw two square on the sides of that triangle. They will both be equal, because the sides of the triangle are equal. Make a diagonal inside those two smaller squares(this figure should look kind of funny . . . !). So, you have four triangles between the two smaller squares; that's the same number of triangles in the larger square. The triangle on top of the square now has two squares on it's right angle sides that sum to the same area as the square on its hypotenuse! This is about as easy a proof of an interesting mathematical fact as you can get!
The above is a linear case of the Pythagorean theorem. Pythagoras(or the Pythagoreans) solved a non-linear case. And more or less showed this theorem is true 'in general.' Pythagoras almost certainly got this also from the Babylonians. Start with a square, and arrange around the inside four right angled triangles. At this stage, you have a square on the inside, which is also 'on' the hypotenuse of each right angles triangle inside. Now, mathematicians of the Babylonians and Pythagoras, rearrange the triangles into two rectangles. I put one rectangle, horizontally, on the upper right hand side . . . and the other, vertically on the lower right hand side. Now, one should probably put an imaginary line from the top rectangles left lower vertex. . . the line should extend from the bottom side of the upper rectangle to the other side of the square. Now, we have a small square in the upper left side, on the small side of the rectangle above. Below, there's a medium sized square on the other right angled side of the lower rectangle.
- Now, for Euclid's famous proof of the Pythagorean theorem, in his then and now monumental axiomiatic unification of all Greek mathematics up to his time. Euclid lived around 300 B.C. and he did his work in the new city and library of Alexandria. Alexander the Great has been dead for a little while. But, the Greeks seemed to be in charge of the whole known world. This was before Alexander the Great's sons started waring with one another, and then the Romans went around cleaning them up from behind. But, anyways!
Before I get to Euclid's theorem, I need to explain all kind of mathematics that needed to be solved before Euclid could see a new more general proof than even the Pythagoreans(the Babylonians).
The simple geometric proof of the area of a triangle is to take a rectangle, or even a square, and divide it in half by a diagonal. The area of the rectangle is of course base times height. Now, we see an extraordinary formula comes out quite simply - the area of a triangle is 1/2base 'x' height. But, triangles can come in a variety of sizes and shapes. Scalene, acute triangles . . . basically, one vertex can extend outside of the base, or well inside. What about these cases? Or, we could say, these are non-linear cases; how to prove them? Euclid breakes it down into every possible case in book one of his Elements - from about 1-35 to 1-41(the Pythagorean theorem is famous 1-47; proved very early in Euclid's elements; what other wonders are in twelve other books? It's noted by mathematicians that Euclid chooses his parallel axiom wisely, and doesn't use it till like book two. Euclid's proof of the Pythagorean theorem is considered a great theorem for this and other reasons).
I won't get into every case; but, what he's doing is showing that when variously, triangles or squares are in the same base and parallels, they have the same areas. You could have a figure like a parallelogram, where there's a small base side, and a longer top side, and hence the two end sides are angled outward. It looks likea bit of a bowl, but with straight lines. Drawing straight parallel lines from the vertices of the bottom base to the opposite end sides generates two overlapping parallelograms. Then through checking off various properties of opposite angles are equal, and similar parts, one sees these paralleograms are of same area. What the Greeks found is that, no matter how skewed the angle of the triangles, the area is the same! Euclid used this property to make a very prove the Pythagorean theorem in general!
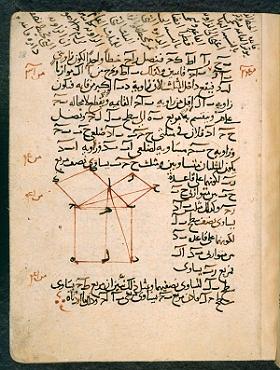
I've generally tried not to put in a picture in this post because they get taken down; but, I can't help putting in a picture of Euclid's famous proof of the Pythagorean theorem,
image credit, The British Library Board
Well, this is a 1200 A.D. Arabic copy of a page of Euclid's Elements, showing Euclid's proof of the Pythagorean theorem. Here, you only see one set of lines relating the rectangle area on the right side to the small square on top. But, the basic idea, and point of it all is as described above.
The Pythagorean theorem makes all kinds of things possible, from making spirals, to number theory of Pythagorean triples, to trigonometry, and differential geometry of Einstein's spacetime. It also leads mankind being able to deal with more non-linear cases of the world - irrational numbers.
Getting back to the linear case of the Pythagorean theorem actually! Where both right angled sides equals one . . . if you make one of those sides base, and both sides equals one . . . then let the hypotenuse fall down on a side, the hypotenuse side extends past whichever base side you choose to a point, that turns out to be an irrational number!
Here's an account of the Pythagorean proof of the irrationality of the square root of 2 that I made elsewhere . . . well, a little more explanation. The algebraic formulation of the Pythagorean theorem is A^2+B^2=C^2 (the "^" means exponent here; I can only hope you know what an exponent means! If not, google it!) In terms of our linear case, with the hypotenuse allowed to fall down on a number line, generating some mystery number, we get 1^2=1^2=C^2, or 1+1=2, and 2=C^2; now, in algebra, to get rid of a exponential, you make a radical sign to both sides . . . the radical sign and the "^2" on the right hand side disappears to just end up with C, and on the other side, you get radical 2, or "what's the square root of 2?"(once again, if you don't know what I'm talking about, just google, square root of 2, or radical sign, or something like that!)
"there's a little theorem of Pythagoras that proves irrational numbers . . . exist! (square root of; or sr)2=a/b(for a rational number, because the Pythagoreans thought all numbers should be these nice little numbers at the most!). Now, in algebra, there's this rule that you can take the radical off a root of a number by squaring it(if this is a root of 2), and squaring the other side, so we get 2=(a^2)/(b^2). Now, some algebraic switcheroo, gives 2(b^2)=a^2. So, a is even, therefore, we can bring in a=2b; so, we substitute this into a^2=2(b^2), so (2b)^2, gives 4b^2=2(b^2) . . . dividing out 2, gives 2b^2!(not the factorial exclamation mark!). We can go the other way, which means b is also even, which means a/b are reducible further . . . which contradicts that a/b is not irreducible; hence, irrational number(in this case the diagonal of a right triangle, which involves the Pythagorean theorem by the way) . . . drumroll . . . exist!|
I don't really want to get into the deductive proof niceties of this proof here. Something I should have said somewhere above when I mentioned deductive proof is . . . Human language is radically different from all other life on Earth. Whether discovered by the Indians(seems to be the case actually!), or the Greeks(they seem to be the first to really take it seriously), deductive proof is as radical an advancement of language, and human reason, and natural human language is over animal language . . . perhaps in my opinion. Here, with the deductive proof of a new number, Human's have unlocked a secret of nature, and gone to a new stage of intelligence(well, the Greeks from Thales on did anyways) Deductive proof unifies, things, it allows one to look behind what our senses immediately tells us(questioning of assumptions), kind of like how our senses say the Earth is flat, and mathematical science allows us to deduce that the Planets goes around the Sun, and not the sun around the Earth. Deductive proof solved problems by showing the balance between two much and two little. It tunes to the exact solution. It shows how things fits exactly. I couldn't stress enough the landmark irrational numbers and the Greek/Pythagorean deduction of it is for mankind. It's like having a spacefship, and parking it in your garage; or, at least it was for these Greeks, who barely wore any clothing at all. It's like some god giving Perecles a sword of some unknown metal never heard of before in "Clash of the Titans(see the original 1981 movie!). Moving on . . . back to Hippocrates 'Quadrature of the Lune' . . . we'll relive the irrational numbers a bit later on though!
- After the Pythagoreans, the next major mathematical milestone was Hippocrates Quadrature of the Lune. The lune is like the crescent phase of the moon. Hippocrates uses 1) the Pythagorean theorem, 2) angles in a semi-circle are right angles, and 3! the areas of two circles, are to one another as the squares on their diameters(Proof is in Euclid's "Elements", book XII-2.
Proof is on a semi-circle, split it in half from the diameters half line . . . on one half(usually on the left side!), draw a straight line from the top of the perpendicular line from the half point of the diameter, to the edge of the diameter on the left side. That should generate a triangle on the left side. On the diameter of triangle, draw a semi-circle. - the angle in the semi-circle is of course, a right angle, so apply the Pythagorean theorem. Well, the legs of the triangle inside the semi circle are of course 1 each, well area of large is 2, while area of small is one, and because of the Euclid XII-2 above, we get 1/2. (AC)^2/2(AC)^2, and the AC's cancel out, leaving 1/2. The bottom is the larger semi-circle, so it's 2 of the semi-circle built on the left side, so it's 1/2, by a theorem that hasn't been proved yet. But, this is how Hippocrates did it!
Hippocrates thought he had proved the area of two circles are as their squares; but, he didn't; he couldn't have. He also thought he had squared the circle. But, he didn't. The crescent is not exactly even squaring one quadrant of the circle! It's something built on top! But, he tried, he did some heptagon thing, which didn't work. This effort was a dead end; but, mathematicians couldn't prove it till like the 1800s when Lindemann proved that Pi is a transcendental number(won't explain here; well, kind of like a curve that intersects a line in the Cartesian plane off to infinity; if you have an algebraic . . . which isn't accurate statement . . . equation that intersects the line off to infinity . . . that's a transcendental number; at that point, you should realize, the Greeks were messing with something far more mathematically scarry than even irrational numbers!). But, I'm going to describe some more mathematics that came out of Hippocrates and the Greeks efforts to square . . . everything, and then get into Archimedes.
Because I'm not really finished with Hippocrates effort to square the lune! Hippocrates showed that the lune on the left side is equivalent to the triangle on the left side. Subtract the left quadrant of the large semi-circle from the small semi-circle built onto the left side; the remainder is the lune(a crescent shape). That cresent in eual to the triangle generated earlier. How is that squared? The Greeks came up with a way to square the triangle.
A triangle is 1/2b'x'h, and a rectangle is of course b'x'h, (I'm using x to mean multiplication; should have explained above!). So, if we make the small side equal to half the height of the triangle, and the base of the rectangle equal to the base of the triangle, we make a rectangle equal in area to the triangle. Then, from there, we make a square equal in area to the rectangle. The squaring of the rectangle involves the Pythagorean theorem. The rectangle long side base is estended to the length of its short side. A square is made where one side is equal to twice the length of the short side of the rectangle. A semi-circle is used to make an intersection point. A triangle is formed, and the Pythagorean theorem is used to equate squares on sides. Some of the geometric algebra looks like EF= FG-EG, BE= BG+GE, these are a-b and a+b respectively. If you take the Pythagorean theorem, you have A^2= B^2 + C^2(I did Pythagorean theorem algebraically wrong above; but, It probably doesn't totally ruin what's said above, fortuitiously), then rearrange the Pythagorean theorem algebraically, to A^2 - B^2 = C^2. Now, more algebra turns the left side into (a-b)(a+b)! Base times Height!
Hipprates once again, proved his theorem, most likely without having proved the different circles are to one another as the squares on their diameters. Remarkable enough, but lets describe some of which is proved in Euclid's elements, hundred plus years after Hippocrates time.
The theorem was most likely observed by the Babylonians, and proved and placed in Euclid's "Elements" XII-2. It relies on two theorems in Euclid's Elements book X-1 and 2. All these proofs are long, and, like describing the proofs above, I'm just going to give the basic ideas of them here. It's like in infinit series, were you have a point at say 1, and you make one point 1/2, the next point 1/4th, and you make half of each succeeding interval that gets closer to the point you want, this is more or less what's done. Actually, there' s a remarkable relation to Euclid's algorithm(subtractive version and not division; there's two versions). You take a smaller part from a larger part, but the smaller part is just more than half the size of the larger, and you repeat the process. X-1 sets up two of these processes and shows them to be equal!
XII-1 is a polygon version of XII-2(circles are to one another as the squares on their diameters). Really, as far as I can tell, all that really happens is that the theorem shows that the squares never exceed certain bounds. XII- 18 is the sphere's version! Archimedes uses this as well. Here, the sphere are to one another as the triplicate ration of their diameters.
Archimedes certainly didn't know you can't square the circle; but, he knew nobody had succeeded. Archimedes by the way got his initial schooling at the Library of Alexandria. He was of nobility. His father was King of Syracuse, on the island of Sicily. I once lived there and more or less saw various things of Syracuse. Sicily has all kinds of ruins going back to pre-Greek and Roman times actually. But, Archimedes lived in a time when the Roman's were consolidating power. They had just defeated the Cartheginians(what was left of the Phoenicians/Minoans. They weren't in the mood for a wise-cracker like Archimedes. Getting back to the mathematics.
Archimedes proved that one can triangulate the circle. He made one side of the triangle equal to the radius of the circle, and the other the circumference of the circle. The areas of the circle equal to the hypotenuse; this last part should suggest he's relating different dimension quantities! But, lets back up to his proving the area of a polygon = 1/2 hQ
Imagine any polygon, send out diameters to each vertex; triangulating the entire polygon. So, for each triangle, 1/2b'x'h+ 1/2b'x'h . . . ; then factor out the b'x'h, and you get 1/2hQ Seems obvious enough!
Getting back to the triangulation of the circle . . . area of triangle is T=1/2rC! (C is of course circumference as one of the triangles dimensional quantities to be multiplied). . . . he makes two cases, 1-A> T. So, 1-A> T would leave an excess. But, one can imagine inscribing a square in the circle, doubling it's sides till it overcomes that excess boundary. So, contradiction. I'm giving a rough description here! But, as always, I'm giving the gist of it. Archimedes then does this in reverse, <, and gets another contradiction; What he's done is a double proof by contradiction!
We have the area of a triangle which is not < or >, but must equal it by deductive proof! Hence, A='Pi'r^2(by the polygonal theorem above!). Or 1/2rC, and plugging in 2'pi'r(circumference, 1/2r(2'pi'r), gives 'pi'r^2
Here, Archimedes sees that he needs to calculate Pi. His plan is to inscribe/circumscribe polygons in/on a circle. This was a plan started by Eudoxus, called method of exhaustion. Eudoxus found the fourth term of proportionality, found in Euclid's Elements book VI I do believe. This is odd, because it's known that book V of Euclid's Elements, all about advanced proportions, is composed by Eudoxus. Eudoxus proves things like A+B/c= D+E/f, and A+B+C.../A'+B'+C'... I mention some more about the genius of Eudoxus in my accounts about Greek Astronomy. But, if you look at inscribing/circumscribing polygons in circles, you'll find that each type of polygon takes a new insight/proof/construction to inscribe and circumscribe around circles! Archimedes finds a proof that allows him to circumvent having to to go through all these different specialized constructions - Euclid's Elements VI-3. I'll describe it later; first, I want to describe some of these constructions!
- To find the center of a circle. Draw a line at your convenience through a circle. Then, bisect it; draw a perpendicular through that bisect point. Then find the bisection of that perpendicular line; that's the center of the circle! The proof is just checkoffs of conditions for it to be so!
I'm just going to describe some inscribing of polygons and not the circumscribing to make this whole writeup a little bit shorter! To inscribe a triangle. Draw a tangeant line to the circle to inscribe the polygon/triangle. Make an angle on one side of the tangeant angle equal to one side of the triangle to inscribe. Then on the other side of the tangeat line, make an angle equal to another angle of the triangle. Then join sides of the angles inside the circle!
A square is the easiest! Draw to lines through the center of the circle, and each perpendicular to each other. Join lines to the the points of intersection between the circle and these lines!
Now, we get the exciting polygon - the Pentagon. This was solved by non other than the Pythagoreans. We inscribe an isosceles triangle like the triangle inscribing method above. Then, make bisection lines from each vertex of that triangle, draw the lines to the other side of the circle. Connect dots by drawing lines from those opposite points to the other points on the circle. Two other iscosceles triangles are generated, by the way. There's actually another way, involving decomposing into triangles.
As the Pythagoreans found out, the Pentagon needed to use certain scaline triangles to decompose it while the other polygons used the same triangles. The Pentagon was a special polygon in that sense. This ability to make a Pentagon was essential to make the Dodecahedron and Icosahedron(the two hardest, and the only really hard ones). Eudoxus also found a proportions method to making the Pentagon.
But, Archimedes actually found a shortcut around having to go through all these polygons and more(he got up to 96 sides; the pentagon in only 5). Euclid's Elements theorem VI-3
If an angle of a triangle be bisected and a straight line cutting the angle cuts the base also, the base will have the same ratio the remaining sides of the triangle. The proof takes a parallel line outside of the triangle, and so uses properties of parallelism as usuall. It basically starts equating angles, even using a few syllogisms, like this angle is equal to this angle, so that first angle is equal to this third angle. So, if you actually check say Sir Thomas Heath's collected works of Archimedes, and see the proof, you'll see a diagram of a quadrant of a circle, with rays coming out of the center point to the circle on the left, and they are all bisecting each other. Which is all great, except, the first one uses a square root of three . . .
Back to the proof of the square root of two. One could do a similar proof for the square root of 3! Thaetetius and a Theodorus did this way back in Athenian times, and went as far as square root of 17. They then did a rather elaborate theory of incommensurability. But, really, we're getting out of subject for this writeup. Archimedes has to make an approximation to this square root of 3. And here, scholars are either mixed, or they just say, they don't know. Nowhere, not Sir Thomas Heath, not Van Der Waerden, not William Dunham, do I ever see anyone actually work this out. They just say, there's two educated guesses of how Archimedes made approximations to this, and three other mystery numbers like this. One way is what's called side and diagonal numbers; modern mathematicians recognize this as a pellian equation of number theory. I quote a passage of Theon of Smyrna, who's actually living around 100 A.D. to give us this account and idea of what Archimedes might have done,
"As the source of all numbers, unity is potentially a side as well as a diagonal. Now let two unts be taken, one lateral unit and one diagonal unit; then a new side is formed by adding the diagonal unit to the lateral unit, and a new diagonal by adding twice the lateral unit to the diagonal unit."
Let's look at the mathematics of this Pythagorean mathematics. Yes, this is yet another piece of Pythagoreanism. This time, they're pretty sure some Pythagorean, and not Pythagoras did this. Pythagoras set up a school of mathematicians. And, they did mathematics. It was probably the first of its kind. A pellian equation is kind of a Pythagorean equation, but like this, d^2=2a^2+/-1
The algebraic generalisations of the Theon description is A(subscript n+1)=A(subscript n)+D(subscript n) , D(subscript n+1)=2a(subscript n)+d(subscript n) . Van Der Waerden gives a educatd guess at a mathematical way the Pythagoreans could have come to this,
Perform an Euclidean algorithm on a triangle. Take a side of a right triangle and subtract it from the hypotenuse. Then, subtract b-a from that smaller side, and so on. From b'=a'-a' , and a'=b-a, we get b'+a'=a (see the algebra from b'=a'-a'? Add +a to both sides, the other one leaves me scratching my head a little bit actually!, and b= 2a'+b' from I see how the 2a' comes from a'= -a, but somehow he fills in b on the 2a' side. There's a mathematical induction performed by the Pythagoreans which seems a bit more solid.
d^2=2a^2+/-1 is proved geometrically in Euclids Elements II-11. The diagram is elaborate, so, I'm going to give a briefer 'model' of what's going on there. Take a straight line, mark acbd, spaced out from left to right. AB is bisected by C, and produced to D, then (AD)^2 + (DB)^2 = 2(AC)^2 + 2(CD)^2. A reexpresing by means of AC=CB=x, BD=y, leads to (2x+y)^2 + Y^2 = 2x^2 + 2(x+y)^2. If you subtract y^2= 2x^2+/-1 from that last equation, you get (2x+y)^2= 2(x+y)^2 +/-1. This I kind of like replacing x by (x+1) in the mathematical induction process. The Pythagoreans had essentially proved their side and diagonal method. And so, now, we can get on to Archimedes calculation of Pi!
All the above is the mathematical history of Pi. Today, we solve it by calculus methods, and some infinit series methods(Vieta has a remarkable trigonometry method). I actually stop here, because, I found that I could not find his first mystery number by the side and diagonal numbers! Archimedes has a 265/153 first approximation to square root of 3. He goes on to far larger fractions. I actually got the 265; but, for some reason, I couldn't get the 153! He uses the Pythagorean theorem, and some of the advanced proportions of Eudoxus to twist and turn numbers as he goes.
I'd like to finish by pointing out that Archimedes goes on to suggest a "cattle of the sungod" problem. Which turns out to be a pellian equation, and even systems of equations. Here's the pellian equation. U^2-(609)(7766)v^2=1. Well, here's a wiki --> Archimedes' cattle problem
- I can't help pointing out more about Archimedes. Everyone knows he came up with the Archimedes screw; there's suggestions he made burning mirror to set ships on fire; but, I'm sure all they did was get in the eyes of the Roman soldiers. They also say he had a mechanical arm that would lift the Roman's ships out of the sea and drop it. That sound's remarkably impractical(would the Roman's allow the Syracusans to hook up the contraption? Mathematically, he did more. He found center points of triangles and ellipses and such. He used Euclid's Elements propostion XII-18 to find areas and volumes of Sphere's like he did for the circle! There's a Heron's area of a triangle formula. A general equation for finding triangular area other than 1/2 b'x'h. It was attributed to Archimedes by the Spanish Arabs. He found the area of a parabola. He used spirals to solve trisection of an angle, he solved third degree equations by means of intersection of conics(today, this wouldn't seem so hard; but, he's doing things by geometric algebra). Getting back to physical science, he found Buoyancy. He helped his King find fraudulent gold by means of density. Well, he supposedly discovered it while bathing, and got out, ran around naked, screaming Eureka! Well, I'm sure back then, people wouldn't have been that disturbed by some guy running around naked in an excited state!
Subscribe to:
Post Comments (Atom)

This comment has been removed by the author.
ReplyDeleteThe mathematical history of the circle above makes a pretty good sweep through ancient mathematics. But, it's not everything. For instance, there's the mathematics of Thales I give in my greek history articles close to the beginning of this blog. Then, I show some great connections between the mathematics found by the Babylonians.
ReplyDeleteThe mathematical history of the conic sections is pretty interesting as well. It wasn't really completed till Descartes.
The Greeks did much more with irrational numbers, and used that knowledge to compute the angles and sides of the platonic solids.
Trigonometry evolved out of the mathematics of Aristarchus and Archimedes.
Today, these mathematics don't strike anyone as extraordinary. As I tried to show of the ancient mathematical history of the circle . . . how it all meant so much more than they do today . . . so with the conic sections and trigonometry.
Theaetetusknot.org/proofs/sq_root.shtml
ReplyDeleteEgyptian calculation of Pi - better than what the Babylonians were able to do(who just approximated it by the Hexagon)
ReplyDelete"For Instance, to find the area of around the field with a diameter of 9 khet (1 khet = 57.2 yards), the area is calculated as follows:-
Take away 1/9th of the diameter, namely 1. The remainder is 8. Multiply it by 8 which gives 64. Therefore, the area will be 64 setjat (unit of area).
In other words, the diameter is equal to 2r, and 1/9 of the radius is (1/9 • 2r), then if we subtract it from the original diameter, we get:
2r — (1/9 • 2r) = 8/9(2r). Then the area of the circle will be 256/81 r². So pi is almost 3.16. They discovered this value of pi almost 4000 years ago."
http://nonagon.org/ExLibris/archimedes-pi - this looks like the best account of Archimedes calculation of Pi. Others make modern trigonometric versions - although these are fascinating in their own right.
ReplyDeleteCalculating π (feat. Archimedes) - https://www.youtube.com/watch?v=K2SeC5ypotY